Horizon Calendars
Even casual observation over a few hours reveals a regular east-to-west motion of celestial objects in the sky, most notably the Sun, due to the Earth's daily rotation. Attentive observations carried out on successive days and weeks soon reveal additional, much slower motions in the Sun, Moon and planets. In particular, the position of the Sun with respect to the "fixed" stars on the celestial sphere varies gradually from day to day, a direct consequence of the Earth's orbital motion around the Sun, as discussed in the last slipe, "The Seasons." Tracking and measuring this seasonal motion is at the core of calendrical practices.
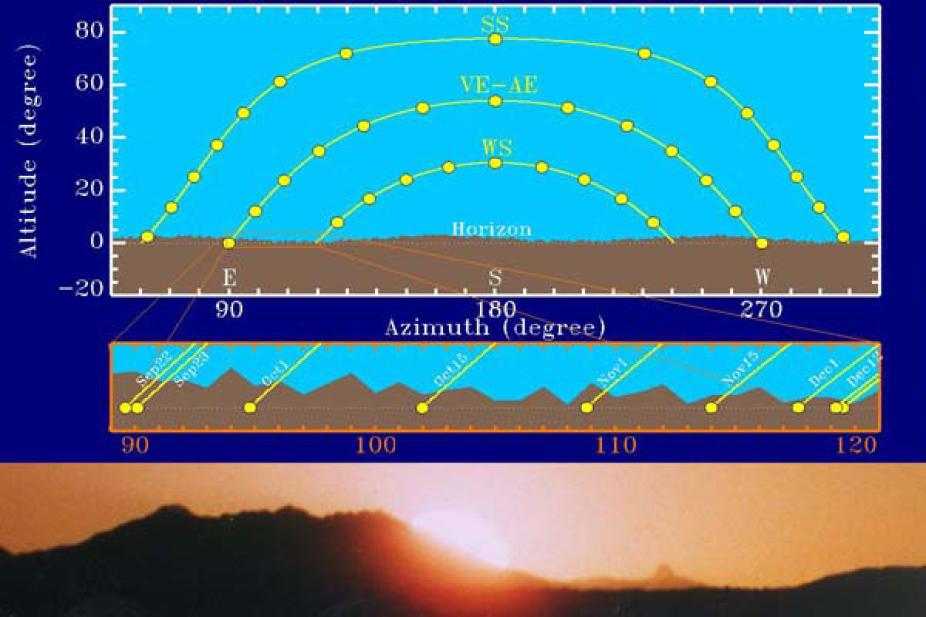
The apparent daily path of the Sun in the sky.
The figure shows a schematic depiction of the apparent daily path of the Sun in the sky at different times of the year, plotted on an azimuth-altitude diagram. The paths were computed for a latitude of 36° and ignoring refraction effects due to the Earth's atmosphere. The top part shows the Sun's path at the summer solstice (SS), winter solstice (WS) and equinoxes (vernal equinox: VE and autumnal equinox: AE; the path is the same for both equinoxes). The small yellow dots indicate the position of the Sun at successive one-hour intervals (with the Sun's diameter expanded by a factor of 10). The Earth's rotation leads to an apparent daily motion of the Sun at a constant angular velocity of 15° per hour; the apparent "acceleration" of the Sun near solar noon (azimuth 180°), especially marked for the SS path, is an artifact of projecting the Sun's circular path on the celestial sphere onto a flat azimuth-altitude plane. The Sun's equinox altitude at solar noon is equal to 90° - Φ, where Φ is the observer's latitude. The equinox-to-solstices altitude differences at solar noon is ± 23.5°, reflecting the inclination of the Earth's spin axis with respect to its orbital axis. Hence, for an observer at 36° latitude the Sun's maximum altitude is 77.5° at summer solstice, 54° at equinoxes, down to only 30.5° at winter solstice. Note also how the day is exactly 12 hours long at equinoxes, up to a little over 14 hours at summer solstice, and down to a little under 10 hours at winter solstice (again for a latitude Φ=36°).
Seasonal change in the Sun's maximum altitude are accompanied by corresponding changes in the azimuths of sunrise and sunset; at the vernal equinox the Sun rises due East; its rising azimuth moves northward until it reaches its northernmost azimuth at the summer solstice. It then moves southward to return to azimuth 90° at the autumnal equinox, and continues southward to its southernmost position, reached at winter solstice. For an observer at 36° latitude, the amplitude of these azimuthal excursions is very nearly 30° on either sides of the equinox (East) azimuth. The setting azimuth moves in an identical fashion about the West direction (azimuth 270°).
This day-to-day displacement of the rising or setting sun along the horizon represents a very practical way to identify the solstices, to be used as reference points in the construction of a calendar. Rather than measuring altitude, one must measure azimuth. For this a gnomon can be used, but it is a lot easier to establish the rising azimuth by noting the position of the rising (or setting) sun against geographical features along the horizon. To avoid the parallax problem, it is preferable to use horizon features located very far away from the observer, and it is necessary to carry out the observations from the exact same location from day to day through the year. This forms the basis of horizon calendars, which represents the most common practice of modern Pueblo people, and most likely of their Anasazi ancestors.
The middle diagram on the slide is a closeup of the region enclosed in orange in the upper diagram. The solar disc is now plotted to scale, with a diameter of a little over half a degree. Notice how the day-to-day horizon displacement decreases rapidly as one approaches solstices (in this case, winter). Sunrise azimuths shifts by an angular distance 10' (=1/6°) per day twenty days before solstices, 5' per day ten days later, and less than 1' per day the last three days before solstice. It has been estimated that the smallest displacement detectable by naked-eye horizon under optimal conditions is at most 4', which occurs eight days before solstices. Consequently, it is not possible to directly establish the day of solstices by naked-eye horizon observation on solstice day. The best way to accurately predict solstices is to track the Sun's displacement 10 to 20 days before the solstices, and count the remaining days.
It is quite likely that the Anasazi living in the ancient town now called Yellow Jacket (Montezuma Basin, Colorado) used the rugged skyline offered by Mt. Wilson (bottom photograph on this slide) in this manner. In particular, on June 5 the Sun rises directly behind Lizard Head Peak, the small horizon feature to the right of the rising Sun on the photograph. This represents a convenient and precise horizon marker to anticipate summer solstice.
Because of the small variations of the Earth's orbital speed about the Sun, due to the orbit's eccentricity, the rising Sun's yearly back-and-forth apparent motion along the horizon is not exactly symmetrical about the E-direction (and, of course, likewise for the variations of sunset azimuth about the W-direction). The effect is small, but not enough to be negligible if attempts are made to time the equinoxes by counting and halving the number of days between solstices, as was apparently done at Hovenweep (next page). While horizon calendars can provide a very accurate means of marking or anticipating solstices and equinoxes, their operation requires that the horizon line contain enough features against which to observe the day-to-day displacement of the rising or setting Sun. If this is not the case, other means must be sought to measure seasonal solar motion.